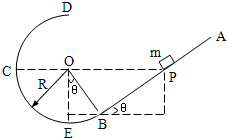
如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可以看作质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因数为μ.求:
(1)物体做往返运动的整个过程中在AB轨道上通过的总路程;
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力;
(3)为使物体能顺利到达圆弧轨道的最高点D,释放点距B点的距离L′应满足什么条件?
(1)因为摩擦始终对物体做负功,所以物体最终在圆心角为2θ的圆弧上往复运动.
对整体过程由动能定理得
mgR•cosθ-μmgcosθ•x=0
所以总路程为x=
.R μ
(2)对B→E过程,由动能定理得
mgR(1-cosθ)=
mvE2-------------------①1 2
FN-mg=m
------------------②V 2E R
由①②得对轨道压力:FN=(3-2cosθ)mg.
(3)设物体刚好到D点,则由向心力公式得
mg=m
------------------③V 2D R
对全过程由动能定理得
mgL′sinθ-μmgcosθ•L′-mgR(1+cosθ)=
mvD2-----------------------④1 2
由③④得最少距离L′=
•R.3+2cosθ 2sinθ-2μcosθ
故答案为:(1)在AB轨道上通过的总路程为x=
.R μ
(2)对圆弧轨道的压力为(3-2cosθ)mg
(3)释放点距B点的距离L′至少为
•R.3+2cosθ 2sinθ-2μcosθ

