问题
解答题
用两条直线最多可以把一个平面分成几部分?3条直线呢?4条直线呢?平面上有(a)4条、(b)5条、(c)6条直线,其中任意两条不平行,任意三条不交于同一点,它们把平面分成几部分?你能总结出什么规律吗?
答案
解:两条直线可以把平面分成4部分。
3条直线(直线相互不平行也不通过同一个点)把平面分成7部分,
作第4条直线,它与前3条直线交于3点,这3点把第4条直线分成4段,相应地平面也就增加了4部分,4条直线把平面分成7+4=11部分作第5条直线,它被分成5段,相应地平面增加5部分,所以5条直线把平面分成7+4+5=16部分,于是6条直线把平面分成7+4+5+6=22部分。事实上,1条直线把平面分成2部分,2条直线把平面分成2+2=4部分,3条直线把平面分成2+2+3=7部分,……,那么n条直线把平面分成2+2+3+4+…+n=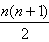 +1部分。
+1部分。
