问题
问答题
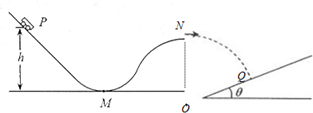
滑板运动是一种陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图是模拟的滑板组合滑行轨道,该轨道由足够长的斜直轨道、半径R的凹形圆弧轨道和半径R的凸形圆弧轨道组成,这三部分轨道处于同一竖直平面内且依次平滑连接,其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心O点与M点处在同一水平面上,一质量为m可看作质点的滑板,从斜直轨道上的P点无初速滑下,经过M点滑向N点,滑板又从N点水平抛出落到一倾角为θ的斜面上的Q点时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示.已知滑板过M点及N点的速度分别为v1和v2(v2<
),不计一切阻力,重力加速度为g.gR
(1)设滑板滑到M点及N点时受到轨道的支持力大小分别为F1和F2,求
=?F1 F2
(2)滑板落到斜面上的Q点时的速度多大?
(3)滑板从N落到斜面上的Q点时所需要的时间为多少?
答案
(1)对M点,根据向心力公式得:
F1-mg=mv 21 R
对N点,根据向心力公式得:
mg-F2=mv 22 R
解以上两式得:
=F1 F2
+gRv 21
-gRv 22
(2)滑板从N点水平抛出垂直斜面到达Q点,根据几何关系得:v=
;v2 sinθ
(3)抛出后做平抛运动,根据几何关系得:vy=
,又vy=gt,v2 tanθ
解得:t=
.v2 gtanθ
答:(1)滑板滑到M点及N点时受到轨道的支持力大小之比
=F1 F2
;
+gRv 21
-gRv 22
(2)滑板落到斜面上的Q点时的速度为
;v2 sinθ
(3)滑板从N落到斜面上的Q点时所需要的时间为
.v2 gtanθ

