如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m的小球，

问题问答题

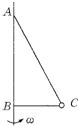
如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m的小球，两绳能承担的最大拉力均为2mg．当AC和BC均拉直时∠ABC=90°，∠ACB=53°，BC=1m．竖直轴AB匀速转动，C球在水平面内做匀速圆周运动．求：

（1）要使两条细绳都拉直，C球的线速度至少多大？

（2）当C球的线速度增大时，AC和BC哪条绳先断？当其中一条绳刚要断时，C球的线速度多大？（g=10m/s²，sin53°=0.8，cos53°=0.6）

答案

（1）当小球线速度增大时，BC逐渐被拉直，小球线速度增至BC刚被拉直时，

对球：T_Asin∠ACB-mg=0…①

T_Acos∠ACB=m

…②

由①②解得：v=

m/s

（2）当绳子拉直时，线速度再增大时，①仍然成立，T_A不变，而T_B增大，所以BC绳先断，当T_B=2mg时，

根据向心力公式得：

2mg+T_Acos∠ACB=m

v′2

③

由①③解得：v′=

110

m/s

答：（1）要使两条细绳都拉直，C球的线速度至少为

m/s；（2）当C球的线速度增大时，BC绳先断，当其中一条绳刚要断时，C球的线速度为

110

m/s．