问题
问答题
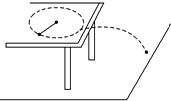
如图所示,一根长为0.1m的细线,一端系着一个质量为0.36kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,当小球的角速度由ω增大到3ω时,细线断裂,这时测得线上的拉力为90N.(g=10m/s2)求:
(1)细线断裂时小球的线速度;
(2)如果桌面高出地面0.8m,线断后小球恰好垂直于桌子右边缘飞出去,求小球落地点离桌面的水平距离为多少?
(3)当小球运动的角速度由ω增到3ω这个过程中,细线上的拉力增大了多少N?
答案
(1)根据F=m
得细线断裂时小球的线速度为:v2 r
v=
=Fr m
=5m/s.90×0.1 0.36
(2)根据h=
gt2得:t=1 2
=2h g
s=0.4s,2×0.8 10
则水平距离为:x=vt=5×0.4m=2m.
(3)根据F=mrω2知,角速度由ω增到3ω这个过程中,绳子拉力变为原来的9倍,
则知当角速度为ω时,绳子拉力为10N,
解得:△F=90N-10N=80N.
答:(1)细线断裂时小球的线速度为5m/s;
(2)小球落地点离桌面的水平距离为2m;
(3)细线的拉力增大为80N.
