问题
问答题
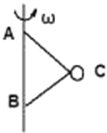
在竖直转轴上有相距1m的A、B两点,A、B两点各通过1m的绳与质量为1kg小球C相连,竖直转轴转动时,小球会跟着以同样的角速度绕轴转动.求:
(1)当竖直转轴以4rad/s转动时,AC绳和BC绳的拉力大小是多少?
(2)当竖直转轴以5rad/s转动时,AC绳和BC绳的拉力大小又是多少?
答案
(1)设BC绳刚好没有拉力时的角速度为ω0,此时由重力和AC绳拉力的合力提供向心力,则有:
mgtan60°=m
Lsin60°ω 20
则得:ω0=
=g Lcos60°
=210 1×0.5
rad/s5
因ω1=4rad/s<ω0时,AC绷直有拉力,BC绳无拉力.
设AC绳与竖直方向的夹角为θ,则有:
mgtanθ=m
lsinθω 21
TAC=mg cosθ
解得:TAC=16N
(2)因ω2=5rad/s>ω0时,AC绳和BC绳均绷直,有拉力,根据牛顿第二定律得:
TACcos60°=mg+TBCcos60°
TACsin60°+TBCsin60°=
Lsin60°ω 22
解得:TAC=22.5N,TBC=3.5N
答:(1)当竖直转轴以4rad/s转动时,AC绳和BC绳的拉力大小分别是16N和0.
(2)当竖直转轴以5rad/s转动时,AC绳和BC绳的拉力大分别为22.5N和3.5N.
