已知f(x)=x2–2x+3,g(x)=kx–1,则“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 ( )
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
题目分析:要是f(x)≥g(x)在R上恒成立,需x2–2x+3≥kx–1,即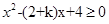 在R上恒成立,所以
在R上恒成立,所以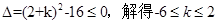 ,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
点评:若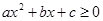
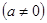 恒成立
恒成立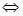
 ;若
;若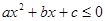
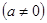 恒成立
恒成立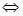
 。
。
已知f(x)=x2–2x+3,g(x)=kx–1,则“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 ( )
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
题目分析:要是f(x)≥g(x)在R上恒成立,需x2–2x+3≥kx–1,即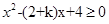 在R上恒成立,所以
在R上恒成立,所以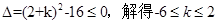 ,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
,所以“| k |≤2”是“f(x)≥g(x)在R上恒成立”的 充分但不必要条件。
点评:若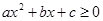
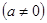 恒成立
恒成立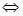
 ;若
;若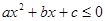
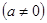 恒成立
恒成立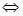
 。
。