如图所示，杆长为L，杆的一端固定一个质量为m的小球，杆的质量忽

问题问答题

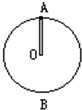
如图所示，杆长为L，杆的一端固定一个质量为m的小球，杆的质量忽略不计，整个系统绕杆的另一端在竖直平面内做圆周运动，求：

（1）小球在最高点A时速度v_A为多大时，才能使杆对小球m的作用力为零？

（2）小球在最高点A时，杆对小球的作用力F为拉力，且大小F=mg，则小球此时的速度是多少？

（3）如m=0.50kg，L=0.5m，v_A=0.4m/s，则在最高点A时，杆对小球的作用力是多大？是推力还是拉力？

答案

（1）杆对小球m的作用力为零时，小球只受重力，由牛顿第二定律有：

mg=m

vA2

得：v_A=

，

（2）小球在最高点时：mg+mg=m

vA2

得：v_A=

2gL

（3）最高点，向心力m

vA2

=0.16N，方向向下，

重mg=5N，方向向下，则杆对球的作用力方向向上，即为推力：F=4.84N；

答：（1）小球在最高点A时速度v_A为

多大时，才能使杆对小球m的作用力为零；

（2）小球在最高点A时，杆对小球的作用力F为拉力，且大小F=mg，则小球此时的速度是

2gL

；

（3）如m=0.50kg，L=0.5m，v_A=0.4m/s，则在最高点A时，杆对小球的作用力是4.84N，是推力．