问题
填空题
已知奇函数f(x)是R上的减函数,且f(3)=-2,设P={x||f(x+t)-1|<1},Q={x|f(x)<-2},若“x∈Q”是“x∈P”的必要不充分条件,则实数t的取值范围是______.
答案
(-∞,-6]
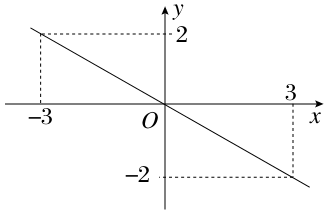
f(x)的图象可以以如图所示的图象为例,则Q={x|x>3}.由|f(x+t)-1|<1,得-1<f(x+t)-1<1,即0<f(x+t)<2,所以-3<x+t<0,所以P={x|-3-t<x<-t}.因为“x∈Q”是“x∈P”的必要不充分条件,所以PQ,3≤-3-t,所以t≤-6.