问题
填空题
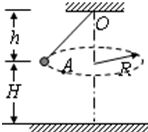
用细线吊着一个小球,使小球在水平面内做半径为R匀速圆周运动;圆周运动的水平面距离悬点h,距离水平地面H.若细线突然在A处断裂,则小球经时间t=______后落地,小球在地面上的落点P与悬点O在水平面上的投影的O,点的距离为______.
答案
设细线与竖直方向上的夹角为θ,小球圆周运动的速度大小为v.
根据牛顿第二定律得:
mgtanθ=mv2 R
又 tanθ=R h
则v=R
.g h
细线突然在A处断裂后小球开始做平抛运动,则:
由 H=
gt2,得 t=1 2
.2H g
则落点P与A点间的水平距离为 x=vt=R
•g h
=R2H g
.2H h
根据几何知识得:小球在地面上的落点P与悬点O在水平面上的投影的O点的距离为:S=
=x2+R2
=R(R
)2+R22H h
.
+12H h
故答案为:
,R2H g
.
+12H h
