问题
解答题
为了求1+2+22+23+…+22008的值,可令S=1+2+22+23+…+22008,则2S=2+22+23+24+…+22009,因此2S-S=22009-1,所以1+2+22+23+…+22008=22009-1
仿照以上推理计算出1+3+32+33+…+32010的值是多少。
答案
解:根据题中的规律,设S=1+3+32+33+…+32010,
则3S=3+32+33+…+32010+32011,
所以3S-S=2S=32011+2,
所以S=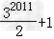
故答案为: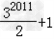 。
。
