问题
问答题
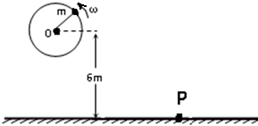
如图所示,一个人用一根长L=1m,只能承受T=46N拉力的绳子,拴着一个质量为m=1kg的小球,在竖直面内做逆时针方向的圆周运动,已知圆心O离地的距离H=6m,g=10m/s2.
(1)此人在小球到达最低点时必须用多大的角速度转动小球方能使绳子被拉断?
(2)若地面上P点停有一只视为质点的乌龟,P点与O点的水平距离为7米,问绳子拉断后,小球第一次着地是否会击中乌龟?如没击中,则小球第一次着地点距乌龟多远?
答案
(1)对小球受力分析,根据牛顿第二定律和向心力的公式可得,
F-mg=mrω2,
所以ω=
=6rad/s.F-mg mr
(2)由v=rω可得,绳断是小球的线速度大小为V=6m/s,
绳断后,小球做平抛运动,
水平方向上:x=v0t
竖直方向上:h=H-L=
gt21 2
代入数值解得 x=6m
小球落地点与抛出点间的水平距离是6m,而P点与O点的水平距离为7米,所以不会击中乌龟,落点距离乌龟x=7-6=1m.
答:(1)此人在小球到达最低点时必须用6rad/s的角速度转动小球方能使绳子被拉断;(2)不会击中乌龟,落点距离乌龟1m.
