问题
问答题
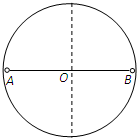
如图所示,内半径为R的光滑圆轨道竖直放置,长度比2R稍小的轻质杆两端各固定一个可视为质点的小球A和B,把轻杆水平放入圆形轨道内,若mA=2m、mB=m,重力加速度为g,现由静止释放两球使其沿圆轨道内壁滑动,当轻杆到达竖直位置时,求:
(1)A、B两球的速度大小;
(2)A球对轨道的压力.
答案
(1)设杆运动到竖直位置时,A、B两球的速度均为v1
对AB系统机械能守恒:mAg•R-mBgR=
(mA+mB)v21 2
解得v=
.
gR2 3
(2)在竖直位置时,设杆对B球的弹力为FNB,轨道对A球的弹力为FNA
对B球mBg+FNB=mBv2 R
解得FNB=-
mg1 3
∴杆对B球有向上的支持力,对A球有向下压力.
对A球:FNA-mAg-
mg=mA1 2 v2 R
解得FNA=
mg11 3
由牛顿第三定律,知A球对轨道的压力为
mg.11 3
答:(1)A、B两球的速度大小为
.
gR2 3
(2)A球对轨道的压力为
mg.11 3
