如图所示，BC为半径R=0.144m的14圆弧，AB为光滑水平轨道，两轨道在B处

问题问答题

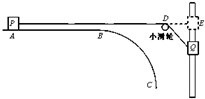
如图所示，BC为半径R=0.144m的

圆弧，AB为光滑水平轨道，两轨道在B处相切连接；AB轨道上的滑块P通过不伸长的轻绳与套在竖直光滑细杆的滑块Q连接；开始时，P在A处，Q在与A同一水平面上的E处，且绳子刚好伸直处于水平，固定的小滑轮在D处，DE=0.4m，不计滑轮与绳子间的摩擦和空气阻力，现把Q从静止释放，当下落h=0.3m时，P恰好到达圆弧轨道的B，且对B无压力．取g=10m/s²．试求：

（1）在P到达B处时，P的速度大小；

（2）在P到达B处时，Q的速度大小；

（3）滑块P、Q的质量之比，即

=？

答案

（1）P恰好到达圆弧轨道的B，且对B无压力，重力提供向心力，根据向心力公式得：

mPg=mP

vP2

解得：vP=

1.44

=1.2m/s

（2）P到达B点时，绳子的速度等于P的速度，根据几何关系有：

vQ•

0.3

0.32+0.42

=vP

解得：vQ=1.2×

0.5

0.3

=2m/s

（3）PQ在运动过程中只有重力做功，根据动能定理得：

mPvP2+

mQvQ2=m_Qgh

带入数据有：

0.72m_P+2m_Q=3m_Q

解得：

0.72

答：（1）在P到达B处时，P的速度大小为1.2m/s；（2）在P到达B处时，Q的速度大小为2m/s；（3）滑块P、Q的质量之比为

0.72

．