问题
计算题
一轻绳两端分别固定在一根竖直棒上相距为L=2.5m的A、B两点,一个质量为m=0.6kg的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上作匀速圆周运动,(θ= 37°g=10m/s2)则
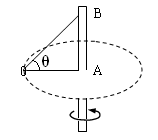
(1)此时轻绳上的张力大小等于多少?
(2)竖直棒转动的角速度为多大?
答案
(1) 10N (2)3rad/s
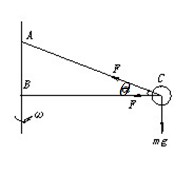
题目分析:(1)如图根据BC水平,由数学知识确定半径的大小,然后受力分析列向心力公式方程.
(2)根据向心力公式以及竖直方向上合外力为零列方程可正确解答本问.
解:
(1)由方程可解得: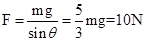 ,又
,又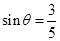
故此时绳的拉力为10N.
(2)环C在水平面内做匀速圆周运动,由于环光滑,所以环两端绳的拉力大小相等.BC段绳水平时,环C做圆周运动的半径r=BC,
则有: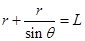 ,解得:
,解得: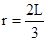
环的受力如图所示,则:
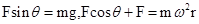
解得: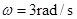
点评:解决圆周运动问题的基本思路是:找圆心,确定半径,对研究对象正确进行受力分析,然后列向心力公式方程.
