问题
选择题
如图所示，有一质量为M的大圆环，半径为R，被一轻杆固定的悬在O点，有两个质量为m的小环（可视为质点），同时从大环两侧的对称位置由静止滑下，两小环同时滑到大环底部时，速度都为v，则此时大环对轻杆的拉力大小为 ( )
A．（2m+2M）g
B．Mg-2mv2/R
C．2m（g+v2/R）+Mg
D．2m（v2/R-g）+Mg
答案
答案：C
题目分析：结合物体状态和受力之间的关系，根据大环的状态--静止，可分析得出大环受平衡力作用；两小环同时滑到大环底部时受向心力作用，根据牛顿第二定律求得小环对大环的弹力．
C、两小环同时滑到大环底部时，小环在竖直方向受重力和弹力，根据牛顿第二定律得：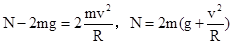
，大环受重力、轻杆拉力和小环对它的压力，根据大环的状态--静止，可分析得出轻杆拉力为
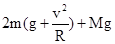．轻因为小环在底部的速度最大，需要的向心力也是最大，所以轻杆拉力也是最大．故C正确．
故选：C．
点评：根据物体的运动状态，分析物体的受力情况是解决此题的关键，另外在分析受力时要考虑周全，不要漏力或添力．