问题
问答题
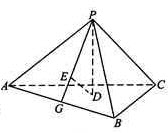
如图，在已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G。
（I）证明：G是AB的中点；
（II）图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积。
答案
参考答案：
（I）因为P在平面ABC内的正投影为D，所以AB⊥PD。
因为D在平面PAB内的正投影为E，所以AB⊥DE。
所以AB⊥平面PED，故AB⊥PG。
又由已知可得，PA=PB，从而G是AB的中点。
（II）在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影。
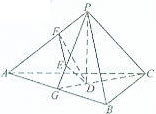
理由如下：由已知可得PB⊥PA，PB⊥PC，又EF∥PB，所以EF⊥PA，EF⊥PC，因此EF⊥平面PAC，即点F为E在平面PAC内的正投影。
连结CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心。
由（I）知，G是AB的中点，所以D在CG上，故CD=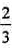
CG。
由题设可得PC⊥平面PAB，DE⊥平面PAB，所以DE∥PC，因此PE=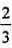
PG，DE=
PC。
由已知，正三菱锥的侧面是直角三角形且PA=6，可得DE=2，PE=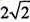
。
在等腰直角三角形EFP中，可得EF=PF=2，所以四面体PDEF的体积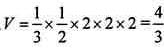
。