问题
问答题
△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c。
（I）求C；
（II）若c=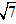
，△ABC的面积为
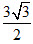，求△ABC的周长。
答案
参考答案：
解：（Ⅰ）由已知及正弦定理得，2cosC（sinAcosB+sinBcosA）=C，
即2cosCsin（A+B）=sinC。
故2sinCcosC=sinC。
可得cos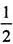C=
，所以C=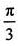
。
（Ⅱ）由已知，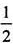
又C=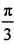
，所以ab=6。
由已知及余弦定理得，a2+b2-2abcosC=7。
故a2+b2=13，从而（a+b）2=25。
所以△ABC周长为5+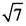
。