问题
问答题
设圆x2+y2+2x-15=0的圆心为A，直线l过点B（1，0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E。
（I）证明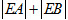
为定值，并写出点E的轨迹方程；
（II）设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围。
答案
参考答案：
（Ⅰ）因为〡AD〡=〡AC〡，EB∥AC，故∠EBD=∠ACD=∠ADC，
所以〡EB〡=〡ED〡，故〡EA〡+〡EB〡=〡EA〡+〡ED〡=〡AD〡。
又圆A的标准方程为（x+1）2+y2=16，从而〡AD〡=4，所以〡EA〡+〡EB〡=4。
由题设得A（-1，0），B（1，0），〡AB〡=2，由椭圆定义可得点E的轨迹方程为：
。
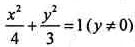（Ⅱ）当l与x轴不垂直时，设l的方程为y=k（x-1）（k≠0），M（x1，y1），N（x2，y2）。
由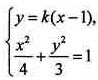
得（4k2+3）x2-8k2x+4k2-12=0。
则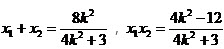
。
所以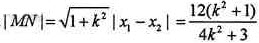
。
过点B（1，0）且与l垂直的直线m：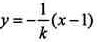
，A到m的距离为
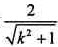，所以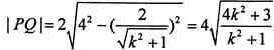
。
故四边形MPNQ的面积
。
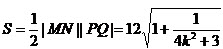可得当l与x轴不垂直时，四边形MPNQ面积的取值范围为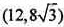
。
当l与x轴垂直时，其方程为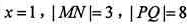
，四边形MPNQ的面积为12。
综上，四边形MPNQ面积的取值范围为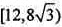
。