问题
问答题
设函数f（x）=（x-1）3-ax-b，x∈R，其中a，b∈R。
（I）求f（x）的单调区间；
（II）若f（x）存在极点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=3；
（III）设a＞0，函数g（x）=∣f（x）∣，求证：g（x）在区间[0，2]上的最大值不小于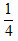
。
答案
参考答案：
搜题请搜索小程序“爱下问搜题”
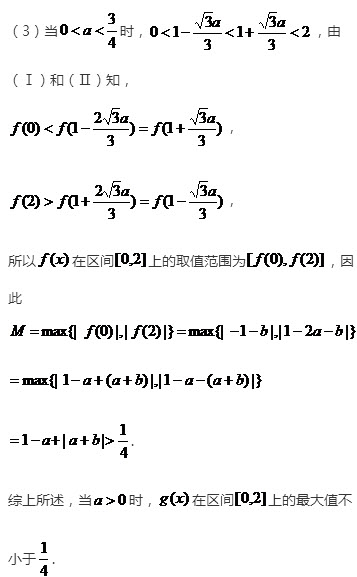
设函数f（x）=（x-1）3-ax-b，x∈R，其中a，b∈R。
（I）求f（x）的单调区间；
（II）若f（x）存在极点x0，且f（x1）=f（x0），其中x1≠x0，求证：x1+2x0=3；
（III）设a＞0，函数g（x）=∣f（x）∣，求证：g（x）在区间[0，2]上的最大值不小于。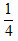
参考答案：