问题
问答题
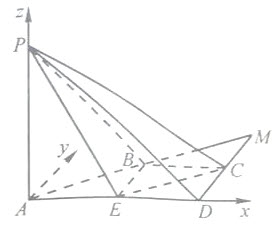
如图，在四棱锥P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=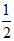
AD。E为边AD的中点，异面直线PA与CD所成的角为90°。
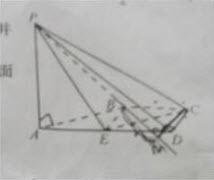
（I）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；
（II）若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值。
答案
参考答案：
（Ⅰ）详见解析；（Ⅱ）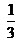
.
解析：
（Ⅱ）方法一：
由已知，CD⊥PA，CD⊥AD，P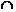A
AD=A，
所以CD⊥平面PAD.
从而CD⊥PD.
所以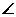
PDA是二面角P-CD-A的平面角.
所以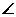PDA=45°.
设BC=1，则在Rt△PAD中，PA=AD=2.
过点A作AH⊥CE，交CE的延长线于点H，连接PH.
易知PA⊥平面ABCD，
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q，则AQ⊥平面PCE.
所以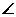APH是PA与平面PCE所成的角.
在Rt△AEH中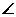，AEH=45°，AE=1，
所以AH=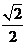
.
在Rt△PAH中，PH=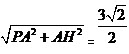
，
所以sin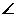
APH=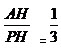
.
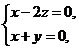
所以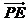
=（1，0，-2），
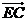=（1，1，0），
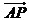=（0，0，2）
设平面PCE的法向量为n=（x，y，z），
由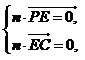
得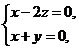设x=2，解得n=（2，-2，1）.
设直线PA与平面PCE所成角为α，则sinα=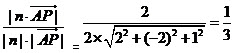
.
所以直线PA与平面PCE所成角的正弦值为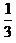
.
考点：线线平行、线面平行、向量法.