问题
问答题
选修4—4：坐标系与参数方程
在直线坐标系xOy中，曲线C1的参数方程为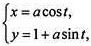
（t为参数，a＞0）。在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=4cosθ。
（I）说明C1是哪一种曲线，并将C1的方程化为极坐标方程；
（II）直线C3的极坐标方程为θ=α0，其中a0满足tanα0=2，若曲线C1与C2的公共点都在C3上，求a。
答案
参考答案：
（I）消去参数t得到C1的普通方程x2+（y-1）2=a2，C1是以（0，1）为圆心，a为半径的圆。
将x=ρcosθ，y=ρsinθ代入C1的普通方程中，得到C1的极坐标方程为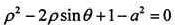
。
（II）曲线C1，C2的公共点的极坐标满足方程组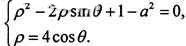
若ρ≠0，由方程组得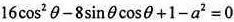
，由已知tanθ=2，可得
，从而1-a2=0，解得a=-1（舍去），a=1。
a=1时，极点也为C1，C2的公共点，在C3上。
所以a=1。