已知函数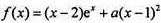 有两个零点。
有两个零点。
(I)求a的取值范围;
(II)设x1,x2是f(x)的两个零点,证明:x1+x2<2。
参考答案:
解:
(Ⅰ) 。
。
(i)设a=0,则f(x)=(x-2)ex,f(x)只有一个零点。
(ii)设a>0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0。
所以f(x)在(-∞,1)单调递减,在(1,+∞)单调递增。
又f(1)=-e,f(2)=a,取b满足b<0且 ,则
,则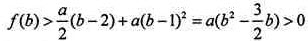 ,
,
故f(x)存在两个零点。
(iii)设a<0,由f′(x)=0得x=1或x=In(-2a)。
若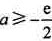 ,则In(-2a)≤1,故当x∈(1,+∞)时,f′(x)>0,因此f(x)在(1,+∞)单调递增。
,则In(-2a)≤1,故当x∈(1,+∞)时,f′(x)>0,因此f(x)在(1,+∞)单调递增。
又当x≤1时f(x)<0,所以f(x)不存在两个零点。
若 ,则In(-2a)>1,故当x∈(1,In(-2a))时,f′(x)<0;当x∈(In(-2a),+∞)时,f′(x)>0。
,则In(-2a)>1,故当x∈(1,In(-2a))时,f′(x)<0;当x∈(In(-2a),+∞)时,f′(x)>0。
因此f(x)在(1,In(-2a))单调递减,在(In(-2a),+∞)单调递增。
又当x≤1时f(x)<0,所以不存在两个零点。
综上,a的取值范围为(0,+∞)。
(Ⅱ)不妨设x1<x2,由(Ⅰ)知,x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1),f(x)在(-∞,1)单调递减,所以x1+x2<2等价于f(x1)>f(2-x2),即f(2-x2)<0。
由于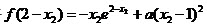 ,而
,而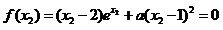 ,所以
,所以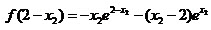 。
。
设 ,则
,则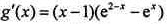 。
。
所以当x>1时,g′(x)<0,而g(1)=0,故当x>1时,g(x)<0。
从而g(x2)=f(2-x2)<0,故x1+x2<2。
