问题
计算题
绳系着装有水的小桶(可当做质点),在竖直平面内做圆周运动,水的质量m=0.5kg,绳长L=60cm,已知重力加速度g=10m/s2。求:
(1)水桶运动到最高点时水不流出的最小速率多大?
(2) 如果运动到最高点时的速率V=3m/s2,水对桶底的压力多大?
(3) 如果运动到最低点时的速率V=3m/s2,水对桶底的压力多大?
答案
(1)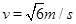 (2)
(2)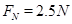 (3)
(3)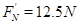
题目分析:(1)在最高点,当水对桶底的压力为零时,此时速度最小,根据牛顿第二定律求出在最高点水不流出的最小速率.
(2)在最高点,水靠重力和桶底对水的压力的合力提供向心力,根据牛顿第二定律求出桶底对水的压力.
解:(1)水跟着水桶一起做圆周运动,要让水不掉出水桶,则在最高点处有:
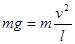
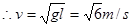
(2)设桶底对水的压力为FN,
则有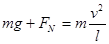 m
m
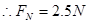
(3)设桶底对水的压力为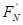 ,
,
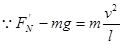
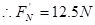
点评:解决本题的关键知道水做圆周运动向心力的来源,根据牛顿第二定律进行求解.
