问题
问答题
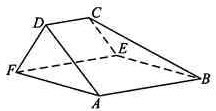
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°。
(I)证明:平面ABEF⊥平面EFDC;
(II)求二面角E-BC-A的余弦值。
答案
参考答案:
解:
(I)由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC。
又AF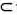 平面ABEF,故平面ABEF⊥平面EFDC。
平面ABEF,故平面ABEF⊥平面EFDC。
(II)过D作DG⊥EF,垂足为G,由(I)知DG⊥平面ABEF。
以G为坐标原点,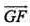 的方向为x轴正方向,
的方向为x轴正方向,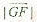 为单位长度,建立如图所示的空间直角坐标系G-xyz。
为单位长度,建立如图所示的空间直角坐标系G-xyz。
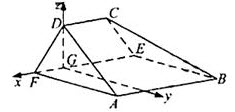
由(I)知∠DFE为二面角D-AF-E的平面角,故∠DFE=60°,则〡DF〡=2,〡DG〡=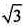 ,可得
,可得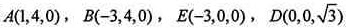 。
。
由已知,AB∥EF,所以AB∥平面EFDC。
又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF。
由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°,从而可得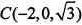 。
。
所以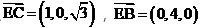 ,
, 。
。
设n=(x,y,z)是平面BCE的法向量,则
 ,
,
所以可取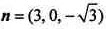 。
。
设m是平面ABCD的法向量,则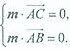 ,
,
同理可取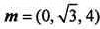 ,则
,则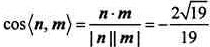 。
。
故二面角E-BC-A的余弦值为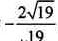 。
。
