某公司计划购买2台机器，该种机器使用三年后即被淘汰。机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元。在机器使用期间，如果备件不足再购买，则每个500元。现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X表示2台机器三年内共需更换的易损零件数，n表示购买2台机器的同时购买的易损零件数。
（I）求X的分布列；
（II）若要求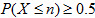
，确定n的最小值；
（III）以购买易损零件所需费用的期望值为决策依据，在n=19与n=20之中选其一，应选用哪个？
参考答案：
解：
（I）由柱状图并以的频率代替概率可得，一台机器在三年内需更换的易损零件数为8，9，10，11的概率分别为0.2，0.4，0.2，0.2。从而
P（x=16）=0.2×0.2=0.04；
P（x=17）=2×0.2×0.4=0.16；
P（x=18）=2×0.2×0.2+0.4×0.4=0.24；
P（x=19）=2×0.2×0.2+2×0.4×0.2=0.24；
P（x=20）=2×0.2×0.4+0.2×0.2=0.2；
P（x=21）=2×0.2×0.2=0.08；
P（x=22）=0.2×0.2=0.04
所以x的分布列为：
（II）由（I）知p（x≤18）=0.44，P（x≤19）=0.68，故n的最小值为19。
（III）记Y表示2台机器在购买易损零件上所需的费用（单位：元）。
当n=19时，
EY=19×200×0.68+（19×200+500）×0.2+（19×200+2×500）×0.08+（19×200+3×500）×0.04=4040。
当n=20时，
EY=20×200×0.88+（20×200+500）×0.08+（20×200+2×500）×0.04=4080。
可知当n=19时所需费用的期望值小于n=20时所需费用的期望值，故应选n=19。
