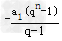(1)观察一列数:-2 ,-4 ,-8 ,-16 ,-32 ,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是______ ;根据这个规律,如果a1表示第1 项,a2表示第2 项,an(n 为正整数)表示这个数列的第n 项,那么a8=________ ,an=________ ;
(2)如果想求l +3 +32+33+…+320的值,可令S = l+3+32+33+…+320………①
将①式两边同乘以3 ,得:________________________________ ………②
由②减去①式,可以求得S =____________________ ;
(3) 用由特殊到一般的方法知:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q ,则a3=___________ (用含a1,q的代数式表示),an=___________ (用含a1,q,n的代数式表示),如果q =2012 ,则a1+a2+…+an= .(用含a1, n的代数式表示)
解:(1)每一项与前一项之比是一个常数,这个常数是2 ,
∴a18=-218 ,an=-2n ;
(2)令s=1+3+32+33+ …+3201
3S=3+32+33+34+ …+3202
3S-S=3202-1
S=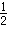 (3202-1) ;
(3202-1) ;
(3)∵第二项开始每一项与前一项之比的常数为q ,
∴an=-a1qn-1,
继而得出: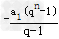
故答案为:2 、-218 、-2n ;3+32+33+34+ …+3202 、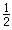 (3202-1) ;-a1qn-1 、
(3202-1) ;-a1qn-1 、