问题
问答题
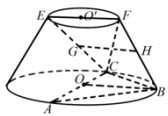
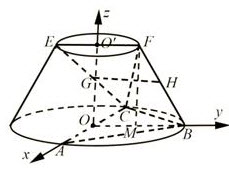
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线。
(I)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(II)已知EF=FB= AC=
AC=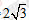 AB=BC。求二面角
AB=BC。求二面角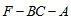 的余弦值。
的余弦值。
答案
参考答案:
(I)证明:设FC的中点为I,连接GI,HI。
在△CEF中,因为点G是CE的中点,所以GI∥EF,又 EF∥OB, 所以GI∥OB。
在△CFB中,因为H是FB的中点,所以HI∥BC, 又HI∩GI=I,所以平面GHI∥平面ABC, 因为GH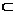 平面GHI,所以GH∥平面ABC。
平面GHI,所以GH∥平面ABC。
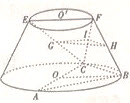
(II)解法一: 连接OO′,则OO′⊥平面ABC, 又AB=BC,且AC是圆O的直径,所以BO⊥AC。
以O为坐标原点,建立如图所示的空间直角坐标系O-xyz, 由题意得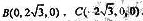 ,过点F作FM垂直OB于点M,
,过点F作FM垂直OB于点M,
所以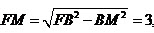 ,可得
,可得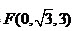 ,故
,故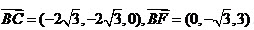 。
。
设m=(x,y,z)是平面BCF的一个法向量。

可得平面BCF的一个法向量 。
。
因为平面ABC的一个法向量n=(0,0,1)。
所以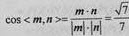 。所以二面角F-BC-A的余弦值为
。所以二面角F-BC-A的余弦值为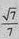 。
。
解法二: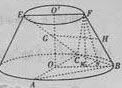
连接OO′,过点F作FM垂直OB于点M, 则有FM∥OO′, 又OO′⊥平面ABC, 所以FM⊥平面ABC,可得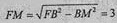 。
。
过点M作MN垂直BC于点N,连接FN, 可得FN⊥BC,从而∠FNM为二面角F-BC-A的平面角。
又AB=BC,AC是圆O的直径, 所以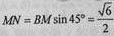 。
。
从而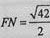 ,可得cos∠FNM=
,可得cos∠FNM=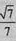 。
。
所以二面角F-BC-A的余弦值为 。
。
