问题
问答题
设数列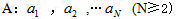
。如果对小于n（2≤n≤N）的每个正整数k都有
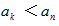，则称n是数列A的一个“G时刻”。记“G（A）是数列A的所有“G时刻”组成的集合。
（I）对数列A：-2，2，-1，1，3，写出G（A）的所有元素；
（II）证明：若数列A中存在an使得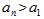
，则
；
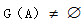（III）证明：若数列A满足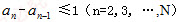
，则G（A）的元素个数不小于
。
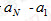答案
参考答案：
（1）G（A）的元素为2和5；（2）详见解析；（3）详见解析.
解析：
如果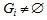
，取
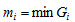，则对任何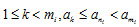
.
从而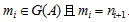
.
又因为np是G（A）中的最大元素，所以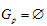
.
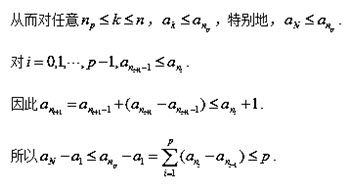
考点：数列、对新定义的理解.