已知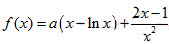 ,a∈R。
,a∈R。
(I)讨论f(x)的单调性;
(II)当a=1时,证明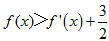 对于任意x∈[1,2]的成立。
对于任意x∈[1,2]的成立。
参考答案:
(Ⅰ)f(x)的定义域为(0,+∞);
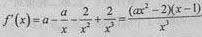 。
。
当a≤0时,x∈(0,1)时,f′(x)>0,f(x)单调递增;
x∈(1,+∞)时,f′(x)<0,f(x)单调递减。
当a>0时,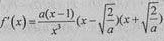 。
。
(1)0<a<2时,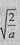 >1,
>1,
当x∈(0,1)或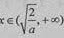 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当x∈(1,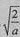 )时,f′(x)<0,f(x)单调递减。
)时,f′(x)<0,f(x)单调递减。
(2)a=2时,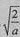 =1,在x∈(0,+∞)内,f′(x)≥0,f(x)单调递增;
=1,在x∈(0,+∞)内,f′(x)≥0,f(x)单调递增;
(3)a>2时,0<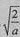 <1,
<1,
当x∈(0,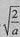 )或x∈(1,+∞)时,f′(x)>0,f(x)单调递增;
)或x∈(1,+∞)时,f′(x)>0,f(x)单调递增;
当x∈(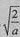 ,1)时,f′(x)<0,f(x)单调递减。
,1)时,f′(x)<0,f(x)单调递减。
综上所述,
当a≤0时,函数f(x)在(0,1)内单调递增,在(1,+∞)内单调递减;
当0<a<2时,f(x)在(0,1)内单调递增,在(1,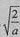 )内单调递减,在(
)内单调递减,在(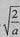 ,+∞)内单调递增;
,+∞)内单调递增;
当a=2时,f(x)在(0,+∞)内单调递增;
当a>2,f(x)在(0,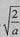 )内单调递增,在(
)内单调递增,在(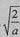 ,1)内单调递减,在(1,+∞)内单调递增。
,1)内单调递减,在(1,+∞)内单调递增。
(Ⅱ)由(Ⅰ)知,a=1时,
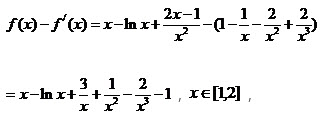 。
。
令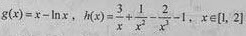 ,
,
则f(x)-f′(x)=g(x)+h(x),
由g′(x)=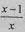 ≥0,可得g(x)≥g(1)=1,当且仅当x=1时取得等号。
≥0,可得g(x)≥g(1)=1,当且仅当x=1时取得等号。
又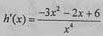 ,
,
设φ(x)=-3x2-2x+6,则φ(x)在x∈[1,2]单调递减,
因为φ(1)=1,φ(2)=-10,
所以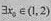 ,使得x∈(1,x0)时,φ(x)>0,x∈(x0,2)时,φ(x)<0。
,使得x∈(1,x0)时,φ(x)>0,x∈(x0,2)时,φ(x)<0。
所以h(x)在(1,x0)内单调递增,在(x0,2)内单调递减。
由h(1)=1,h(2)= ,可得h(x)≥h(2)=
,可得h(x)≥h(2)= ,
,
当且仅当x=2取得等号,所以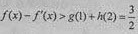 ,即
,即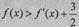 对于任意的x∈[1,2]成立。
对于任意的x∈[1,2]成立。
