问题
问答题
平面直角坐标系xOy中，椭圆C：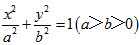
的离心率是
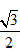，抛物线E：x2=2y的焦点F是C的一个顶点。
（I）求椭圆C的方程；
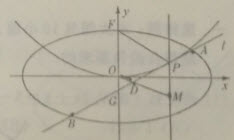
（II）设P是E上的动点，且位于第一象限，E在点P处的切线l与C交与不同的两点A，B，线段AB的中点为D，直线OD与过P且垂直于x轴的直线交于点M。
（i）求证：点M在定直线上；
（ii）直线l与y轴交于点G，记△PFG的面积为S1，△PDM的面积为S2，求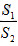
的最大值及取得最大值时点P的坐标。
答案
参考答案：
（Ⅰ）由题意知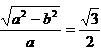
，可得：a=2b。
因为抛物线E的焦点F（0，
），所以b=
，a=1。
所以椭圆C的方程为x2+4y2=1。
（Ⅱ）（i）设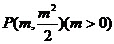
，由x2=2y，可得y′=x，
所以直线l的斜率为m。
因此直线l的方程为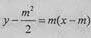
，即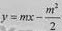
。
设A（x1，y1），B（x2，y2），D（x0，y0），联立方程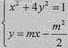
，
得（4m2+1）x2-4m3x+m4-1=0。
由△>0，得
。
且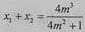
，
因此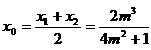
。
将其代入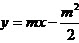
得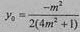
，
因为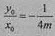
，所以直线OD方程为
。
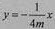联立方程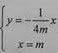
，得点M的纵坐标为
，
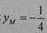所以点M在定直线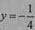
上。
（ii）由（i）知直线l方程为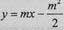
，
令x=0，得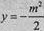
，所以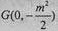
。
又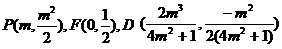
，
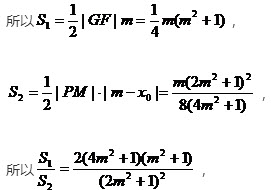
设t=2m2+1，则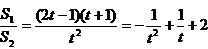
，
当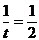
，即t=2时，
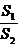取得最大值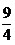
，此时m=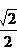
，满足△>0，
所以点P的坐标为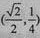
，因此
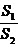的最大值为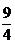
，此时点的坐标为
。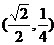