问题
问答题
如图，在四棱锥P-ABCD中，平面
平面ABCD，
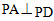，PA=PD，
，
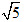（I）求证：平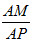
面PAB；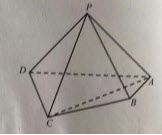
（II）求直线PB与平面PCD所成角的正弦值；
（III）在棱PA上是否存在点M，使得BMll平面PCD若存在，求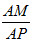的值；若不存在，说明理由。
答案
参考答案：
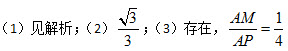
解析：
试题分析：（1）由面面垂直性质定理知AB⊥平面PAD；根据线面垂直性质定理可知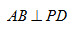
，再由线面垂直判定定理可知PD⊥平面PAB；（2）取AD的中点O，连结PO，CO，以O为坐标原点建立空间直角坐标系O-xyz，利用向量法可求出直线PB与平面PCD所成角的正弦值；（3）假设存在，根据A，P，M三点共线，设
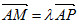，根据
平面PCD，即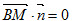
，求λ的值，即可求出
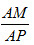的值.
试题解析：（1）因为平面PAD⊥平面ABCD，AB⊥AD，
所以AB⊥平面PAD，所以AB⊥PD，
又因为PA⊥PD，所以PD⊥平面PAB；
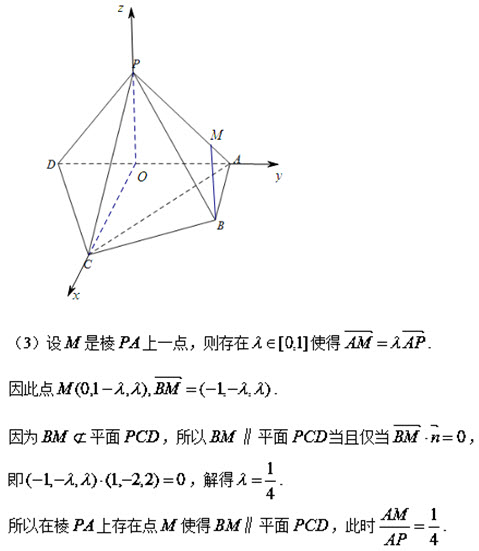
考点：1.空间垂直判定与性质；2.异面直线所成角的计算；3.空间向量的运用.