问题
问答题
（一）选修4-1：几何证明选讲
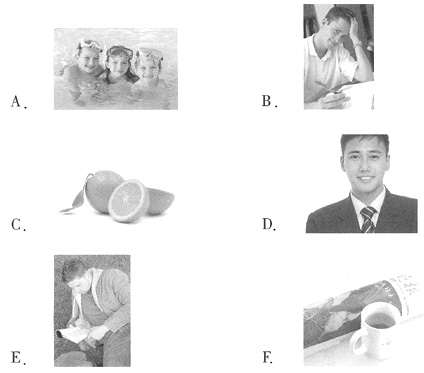
如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F。
（Ⅰ）证明：B，C，G，F四点共圆；
（Ⅱ）若AB=1，E为DA的中点，求四边形BCGF的面积。
答案
参考答案：
（I）因为DF⊥EC，所以△DEF ∽△CDF，则有
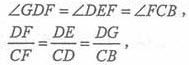
所以△DGF ∽△CBF，由此可得∠DGF=∠CBF。
由此∠CGF+∠CBF=180°，所以B，C，G，F四点共圆。
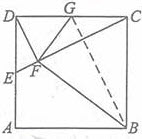
（II）由B，C，G，F四点共圆，CG⊥CB知FG⊥FB，连结GB。
由G为Rt△DFC斜边CD的中点，知GF=GC，故
，因此，四边形BCGF的面积S是△GCB面积S△GCB的2倍，即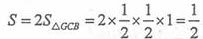
。