问题
计算题
如图所示，A、B两个齿轮的齿数分别是z1、z2，各自固定在过O1、O2的轴上，其中过O1的轴与电动机相连接，此轴转速为n1，求：
(1)B齿轮的转速n2；
(2)A、B两齿轮的半径之比；
(3)在时间t内，A、B两齿轮转过的角度之比，以及B齿轮外缘上一点通过的路程。
答案
解：在齿轮传动装置中，各齿轮的“齿”是相同的，齿轮的齿数对应齿轮的周长，在齿轮传动进行转速变换时，单位时间内每个齿轮转过的齿数相等，相当于每个接合的齿轮边缘处线速度大小相等，因此齿轮传动满足的关系是齿轮转速与齿数成反比，即
(1)齿轮的转速与齿数成反比，所以B齿轮的转速n2=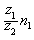
(2)齿轮A边缘的线速度v1=ω1r1=2πn1r1
齿轮B边缘的线速度v2=ω2r2=2πn2r2
因两齿轮边缘上点的线速度大小相等，即v1=v2
所以2πn1r1=2πn2r2
即两齿轮半径之比r1：r2=n2：n1=z1：z2
(3)在时间t内A、B转过的角度分别为φ1=ω1t=2πn1t，φ2=ω2t=2πn2t
转过的角度之比φ1：φ2=n1：n2=z2：z1
B齿轮外缘上一点在时间t内通过的路程为sB=v2t=ω2r2t=2πn2r2t=2πz1n1r2t/z2