问题
问答题
已知A是椭圆E: =1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,
=1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上, 。
。
(I)当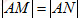 时,求△AMN的面积。
时,求△AMN的面积。
(II)当2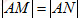 时,证明:
时,证明: 。
。
答案
参考答案:
(Ⅰ)设M(x1,y1),则由题意知y1>0。
由已知及椭圆的对称性知,直线AM的倾斜角为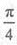 。
。
又A(-2,0),因此直线AM的方程为y=x+2。
将x=y-2代入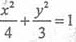 得7y2-12y=0。
得7y2-12y=0。
解得y=0或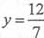 ,所以
,所以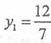 。
。
因此△AMN的面积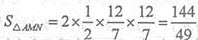 。
。
(2)将直线AM的方程y=k(x+2)(k>0)代入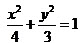 得
得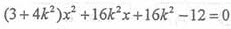 。
。
由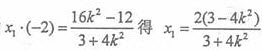 ,故
,故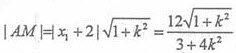 。
。
由题设,直线AN的方程为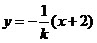 ,故同理可得
,故同理可得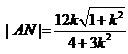 。
。
由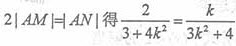 ,即4k3-6k2+3k-8=0。
,即4k3-6k2+3k-8=0。
设f(t)=4t3-6t2+3t-8,则k是f(t)的零点。
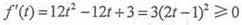 ,所以f(t)在(0,+∞)单调递增,又
,所以f(t)在(0,+∞)单调递增,又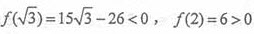 , 因此f(t)在(0,+∞)有唯一的零点,且零点k在
, 因此f(t)在(0,+∞)有唯一的零点,且零点k在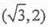 内,所以
内,所以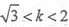 。
。
