问题
问答题 计算题
已知曲线y＝x(1-lnx)，过点(e，0)的曲线的切线、法线与直线y＝a所围成三角形的面积为e2，求a．
答案
参考答案：
由已知条件，y'＝(1-lnx)-1＝-1nx．
所以过点(e，0)的曲线切线斜率
k＝y'|x＝e ＝-1
于是，如图6-1，过点(e，0)的曲线的切线方程、法线方程分别是
y＝-x+e，y＝x-e
直线y＝a与曲线切线、法线的交点坐标为A(e-a，a)， B(e+a，a)．可知A，B相距|AB|＝20．所以△ABC的面积S＝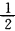
(20·a＝a2＝e2．得d＝e或a＝-e，