问题
单项选择题
已知两个浮点数,阶码为3位二进制数,尾数为5位二进制数,均用补码表示。
[X]补=0.1101×2001,[y]补=1.0111×2011
则两个数的和[x+y]补= (1) ,并说明规格化数的要求是 (2) 。
(2)处填()。
A.阶码之值在阶数可表示的范围内
B.尾数之值在尾数可表示的范围内
C.结果尾数之绝对值≥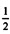
D.尾数之最高数值位=1
答案
参考答案:C
解析:
浮点数[x]补+[y]补=[x+y]补
[x]补=0.1101×2001
[y]补=1.0110×2011
浮点加法第1步必须对阶求阶差:
△E=Ex-Ey=001-011=[001]补+[-011]补=110 即-2
x为小阶的数,x的阶应取大阶阶码:
[*]
第2步 尾数相加[*]
(Mz)补=00.001101+11.0110=11.100101,Ez=011
第3步 规格化,规格化要求结果尾数的绝对值≥[*],现在尾数和的最高数值位为非有效位,绝对值<[*],需左规1位,阶码减1,即:
[*]
第4步 舍入,采用恒置1法。将最末位的1舍去(只能取4位尾数的值),再将尾数末位变成1,[*]
第5步 测溢出。浮点数判断溢出,主要看结果的阶码是否超出了阶码能表示的范围。
浮点数的阶码为3位补码,最大值是+3,最小值是斗,现在结果的阶码为+2,在阶码允许范围之内,所以浮点数不溢出。
