问题
单项选择题
已知p，q均为质数，且满足5p2+3q＝59，则以p+3，1-p+q，2p+q-4为边长的三角形是（）。
A．锐角三角形
B．直角三角形
C．全等三角形
D．钝角三角形
E．等腰三角形
答案
参考答案：B
解析：
[分析]： 5p2+3q为奇数，故p，q一奇一偶，而p，q均为质数，从而p，q中有一个是2，若q＝ 2，则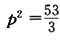
，不合题意，从而必有p＝2，q＝13，此时
p+3＝5，1-p+q＝12，2p+q-4＝13
因为 52+122＝132，从而三角形为直角三角形。