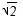问题
单项选择题
已知函数y＝f（x）对一切x满足xf"（x）+3x[f'（x）]2＝1-e-x．若f'（x0）＝0（x0≠0），则（）．
A．f(x0)是f的极大值
B．f(x0)是f的极小值
C．(x0，f(x0))是曲线)y＝f的拐点
D．以上结论均不正确
答案
参考答案：B
解析：
由F'(x0)＝0可知，x＝x0是y＝f(x)的驻点．又x0f"(x0)＝1-．所以
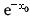
当x0＞0时，
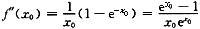＞1；当x0＜0时，0＜＜1．故总有
f"(x0)＞0
所以x＝x0为极小值点，f(x0)为极小值．