问题
单项选择题
已知|x|≤1，|y|≤1，且z＝|x+y|+|y+1|+|x-2y+4|，z的最大值为M，z的最小值为m，则（）。
A．M＝6，m＝3
B．M＝7，m＝3
C．M＝7，m＝2
D．M＝6，m＝2
E．M＝7，m＝0
答案
参考答案：B
解析：
由|y|≤1，得|y+1|＝y+1， 又 -2≤2y≤2， -1≤x≤1， 所以 -3≤x-2y≤3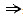
x-2y+4＞0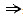|x-2y+4|＝x-2y+4． 则 z＝|x+y|+y+1+x-2y+4＝|x+y|+x-y+5． 当x+y≥0时，z＝2x+5，|x|≤1，3≤z≤7． 当x+y＜0时，z＝5-2y，由|y|≤1，所以3≤z≤7． 所以M＝7，m＝3．故选(B)．
