问题
单项选择题
x，y是关于t的方程t2-2at+a+2=0的两个实根，那么x2+y2的最小值是（）。
A．
B．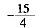
C．8
D．0
E．2
答案
参考答案：E
解析：
由△=(2a)2-4(a+2)≥0得a≥2或a≤-1；x2+y2=(x+y)2-2xy=4a2-2a-4=[*]，当a=-1时取得最小值2。
搜题请搜索小程序“爱下问搜题”
x，y是关于t的方程t2-2at+a+2=0的两个实根，那么x2+y2的最小值是（）。
A．
B．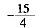
C．8
D．0
E．2
参考答案：E
解析：
由△=(2a)2-4(a+2)≥0得a≥2或a≤-1；x2+y2=(x+y)2-2xy=4a2-2a-4=[*]，当a=-1时取得最小值2。