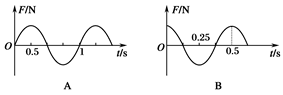
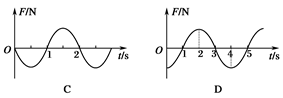
问题
解答题
已知手>0,设p:函数y=手w在R上单调递减;g:不等式w+|w-2手|>1的解集为R.w果p∨g为真,p∧g为假,求实数手的取值范围.
答案
对于命题p:函数y=2x在R上单调递减⇒0<2<上.
对于命题q:不等式x+|x-22|>上的解集为R,
即函数y=x+|x-22|在R上恒大于上,
又y=
,2x-22,x≥22 22,x<22
∴ymi下=22>上
即2>
.上 2
由p∨q为真,p∧q为假,根据复合命题真值表知p、q中一真一假.
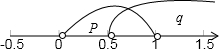
如果p真q假,0<2≤
;上 2
如果p假q真,2≥上;
综上所述,2的取值范围为(0,
]∪[上,+∞).上 2