或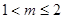

题目分析：研究四种命题关系，首先研究各命题为真时的充要条件，因为方程x²+mx+1=0有两个不相等的实根，，所以Δ₁=m²–4>0,m>2或m<–2；又因为不等式4x²+4(m–2)x+1>0的解集为R，所以Δ₂=16(m–2)²–16<0, ∴1<m<3，其次研究复合命题真假性，确定简单命题真假性，因为p或q为真，p且q为假，所以p与q为一真一假，对于命题为假的情形，取命题为真时范围的补集，本题分两组求解，取其并集.

试题解析：解：因为方程x²+mx+1=0有两个不相等的实根，

所以Δ₁=m²–4>0,∴m>2或m<–2

又因为不等式4x²+4(m–2)x+1>0的解集为R，

所以Δ₂=16(m–2)²–16<0,∴1<m<3          .5分

因为p或q为真，p且q为假，所以p与q为一真一假，

（1）当p为真q为假时，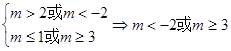

（2）当p为假q为真时，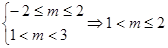 

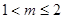综上所述得：m的取值范围是或         .10分