问题
解答题
已知命题p：方程2x2＋ax－a2＝0在[－1,1]上有解；命题q：只有一个实数x0满足不等式x02＋2ax0＋2a≤0，若命题“p∨q”是假命题，求实数a的取值范围．
答案
(－∞，－2)∪(2，＋∞)
解：由2x2＋ax－a2＝0得(2x－a)(x＋a)＝0，
∴x＝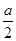
或x＝－a，
∴当命题p为真命题时|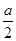|≤1或|－a|≤1，∴|a|≤2.
又“只有一个实数x0满足x02＋2ax0＋2a≤0”，
即抛物线y＝x2＋2ax＋2a与x轴只有一个交点，
∴Δ＝4a2－8a＝0，∴a＝0或a＝2.
∴当命题q为真命题时，a＝0或a＝2.
∵命题“p∨q”为假命题，∴p假q假，∴|a|>2，∴a>2或a<－2.
即a的取值范围为(－∞，－2)∪(2，＋∞)．