问题
解答题
已知命题P:函数y=loga(1-2x)在定义域上单调递增;命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若P∨Q是真命题,求实数a的取值范围.
答案
(-2,2]
解:命题P:函数y=loga(1-2x)在定义域上单调递增,
∴0<a<1.
又∵命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立,
∴a=2或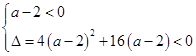
即-2<a≤2.
∵P∨Q是真命题,
∴a的取值范围是(-2,2].
