问题
解答题
设命题p：函数f(x)＝lg(ax2－4x＋a)的定义域为R；命题q：不等式2x2＋x>2＋ax，在x∈(－∞，－1)上恒成立，如果命题“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．
答案
[1,2]
解：p：Δ<0且a>0，故a>2；
q：a>2x－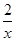
＋1对∀x∈(－∞，－1)恒成立，
设g(x)＝2x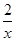－＋1，
则g(x)在(－∞，－1)上单调递增，g(x)<1，故a≥1.
“p∨q”为真命题，命题“p∧q”为假命题，等价于p，q一真一假．
故1≤a≤2，则实数a的取值范围为[1,2]．