问题
证明题
已知函数f(x)在（-∞，+∞）上是增函数，a、b∈R，对命题若a+b≥0，则f(a）+f(b)≥f(-a）+f（-b）”．
(1)写出逆命题，判断其真假，并证明你的结论；
(2)写出逆否命题，判断其真假，并证明你的结论．
答案
（1）逆命题：若f（a）+f（b）≥f（-a）+f（-b），则a+b≥0，为真命题．
用间接法证明：
假设a+b<0，则a<-b，b<-a．
∵f（x）在（-∞，+∞）上为增函数，则f（a）< f（-b），f（b）<f（-a），
∴f（a）+f（b）<f（-a）+f（-b）．
这与题设相矛盾，所以逆命题为真命题．
（2）逆否命题：若f（a）+f（b）<f（-a）+f（-b），则a+b<0，为真命题．因为一个命题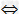
它的逆否命题，所以可证明原命题为真命题，
∵a+b≥0，
∴a≥-b,b≥-a
又∵f（x）在（-∞，+∞）上是增函数，
∴f（a）≥f（-b），f（b）≥f（-a），
∴f（a）+f（b）≥f（-a）+ f（-b），
所以逆否命题为真命题．