问题
解答题
若m∈R，命题p：设x1和x2是方程x2﹣ax﹣3=0的两个实根，不等m2﹣2m﹣4≥|x1﹣x2|对任意实数a∈[﹣2，2]恒成立命题q：“4x+m＜0”是“x2﹣x﹣2＞0”的充分不必要条件．求使p且￢q为真命题的m的取值范围．
答案
解：∵x1，x2是方程x2﹣ax﹣3=0的两个实根
∴x1+x2=a，x1x2=﹣3
∴|x1﹣x2|=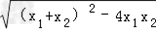
=
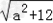
∵a∈[﹣2，2]
∴
∈[2
，4]
∵不等m2﹣2m﹣4≥|x1﹣x2|对任意实数a∈[﹣2，2]恒成立
∴m2﹣2m﹣4≥|x1﹣x2|max在a∈[﹣2，2]成立即可
∴m2﹣2m﹣4≥4解得m≤﹣2或m≥4
∴p：m≤﹣2或m≥4
∵x2﹣x﹣2＞0 ∴x＜﹣1或x＞2
∵4x+m＜0∴x＜﹣
∵“4x+m＜0”是“x2﹣x﹣2＞0”的充分不必要条件
∴﹣
＜﹣1解得m＞4
∴q：m＞4
∵p且￢q为真命题
∴{m|m≤﹣2或m≥4}∩{m|m≤4}={m|m≤﹣2或m=4}