问题
解答题
已知a＞1，命题p：a（x-2）+1＞0，命题q：（x-1）2＞a（x-2）+1＞0．若命题p、q同时成立，求x的取值范围．
答案
解：依题意，命题p、q同时成立，
说明不等式组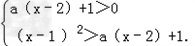
解集为非空集合，
即
解集非空，
结合已知条件a＞1，解得
①当1＜a＜2时，则有
，
而a﹣（2﹣
）=a+
﹣2＞0，即a＞2﹣
，
∴不等式组的解为：x＞2或2﹣
＜x＜a．
因此，此时x的取值范围为（2﹣
，a）∪（2，+∞）．
②当a=2时，则x＞
且x≠2，此时x的取值范围为（
，2）∪（2，+∞）．
③当a＞2时，则有
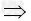x＞a或2﹣
＜x＜2．
因此，此时x的取值范围为（2﹣
，2）∪（a，+∞）．