问题
解答题
已知下列两个命题：P：函数f（x）=x2﹣2mx+4（m∈R）在[2，+∞）单调递增；Q：关于x的不等式4x2+4（m﹣2）x+1＞0（m∈R）的解集为R；若P∨Q为真命题，P∧Q为假命题，求m的取值范围．
答案
解：函数f（x）=x2﹣2mx+4（m∈R）的对称轴为x=m，
故P为真命题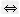
m≤2；
Q为真命题
△=[4（m﹣2）]2﹣4×4×1＜0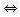
1＜m＜3；
又∵P∨Q为真，P∧Q为假，
∴P与Q一真一假；
若P真Q假，则
，∴m≤1；
若P假Q真，则
，∴2＜m＜3；
综上所述，m的取值范围{m|m≤1或2＜m＜3}．